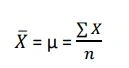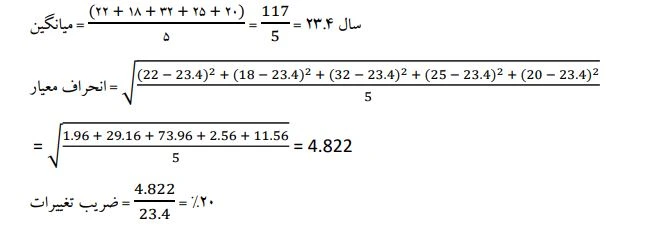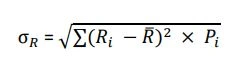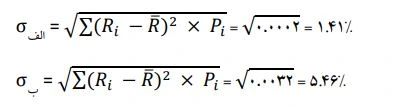با پیشرفت سرمایهگذاری و فراگیری آن در دنیا، نیاز به علمی کردن راه و روشهای اندازهگیری سود، زیان، ریسک، خطرات و … در بازار سرمایه بیشتر شد. علوم زیادی در این راه مورد استفاده قرار گرفت، از حسابداری گرفته تا روانشناسی و آمار.
در سالهای اخیر علم آمار و احتمالات کاربرد غیرقابل انکاری در حوزهی تعیین ریسک برای بازارهای مالی پیدا کرده است.
سبدگردانی و معاملهگری مدرن، روزبهروز وابستگی بیشتری به آمار پیدا میکنند و این در نتایج مثبت ایشان هم کاملاً هویدا است. ضریب تغییرات یکی از عوامل کاربردی آمار در حوزهی مدیریت پرتفوی و سبدگردانی است. در این مقاله به این موضوع خواهیم پرداخت.
ضریب تغییرات چیست؟
ضریب تغییرات (Coefficient Variation) یا CV (بعضاً آن را با COV هم نمایش میدهند) معیاری آماری از پراکندگی نقاط داده در حول میانگین است. به عبارتی اگر یک تعداد دادهی مشخص داشته باشیم، برای به دست آوردن ضریب تغییرات آن، باید ابتدا میانگین را پیدا کرده و سپس میزان پراکندگی دادهها نسبت به این میانگین را محاسبه نمود.
ضریب تغییرات یک معیار آماری مفید برای مقایسه میزان تفاوتها در میان چند سری داده است. حتی اگر میانگین آنها به شدت باهم متفاوت باشند. ضریب تغییرات نشاندهندهی نسبت انحراف استاندارد دادهها به میانگین است.
در آمار و احتمالات، ضریب تغییرات را “انحراف معیار (استاندارد) نسبی” (Relative Standard Deviation) یا RSD نیز مینامند. به لحاظ آماری، ضریب تغییرات را میتوان معیاری استاندارد برای تعیین پراکندگی توزیع احتمال نامید.
برخلاف انحراف معیار که همیشه باید در زمینه میانگین داده ها در نظر گرفته شود، ضریب تغییرات ابزار نسبتاً ساده و سریعی را برای مقایسه سری های مختلف داده ارائه می دهد.
این معیار اغلب به صورت درصدی بیان میشود، که نسبت (Ratio) انحراف معیار استاندارد (σ) به میانگین (μ) را محاسبه مینماید.
مفهوم ضریب تغییرات
ضریب تغییرات میزان تنوع دادههای یک جامعه آماری را، نسبت به میانگین آن جامعه آماری نشان میدهد. در حالت ایدهآل، اگر فرمول ضریب تغییرات به نسبت کمتری از انحراف معیار میانگین بازده منجر شود، در این صورت توازن ریسک و بازده در حالت کاملاً مناسبی قرار دارد و بهتر است.
هرچه میزان ضریب تغییرات کمتر باشد، به معنی این است که پراکندگی در اطراف نقطه میانگین کمتر است و دادهها یکدستتر هستند. هرچه هم میزان ضریب تغییرات بالاتر باشد، نشانهی پراکندگی و فاصلهی بیشتر دادهها از میانگین است.
از محاسبهی ضریب تغییرات، میتوان برای اندازهگیری انحراف بین میانگین قیمت تاریخی و قیمت فعلی یک سهم، کالا یا انواع اوراق قرضه نسبت به سایر داراییها نیز استفاده کرد.
کاربرد ضریب تغییرات چیست؟
ضریب تغییرات به صورت گسترده در شیمی تجزیه، برای اطمینان از دقت آزمایشات و حصول اطمینان از تکرارپذیر بودن نتیجه استفاده میشود. همچنین در زمینهی مهندسی و فیزیک برای انجام بررسیهای تضمین کیفیت داده و انجام تستهای ANOVA (Analysis Of Variance) استفادهی فراوان دارد.
ANOVA به صورت خلاصه به معنی سنجش صحت دادهها است. در این روش آماری، ابتدا آن تحقیقات مشخص (که مورد آزمون است) را با دادههایی متفاوت محاسبه میکنند. پس از انجام آزمایش، نتایج به دست آمده را ثبت میکنند و در اینجا اصل کار آماری ANOVA شروع میشود.
سپس بررسی میکنند که این نتایج عملی حاصل از آزمونهای مختلف با دادههای متفاوت، چه میزان پراکندگی با نتایج مورد انتظار از تئوری اصلی دارد. اگر این پراکندگی بیش از حد استاندارد بود، آن آزمایش خطای زیادی دارد و مورد قبول واقع نمیشود.
به بیان خلاصهتر، ANOVA میزان دادههای پرت را محاسبه میکند و در صورت زیاد بودن آنها، آزمایش را مردود میکند. این آزمون یکی از موارد مهم در روشهای آماری SPSS است و در آزمایشگاهها و همچنین تحقیقات بینالمللی و پایاننامههای دانشگاهی، کاربرد اساسیای در صحتسنجی آزمایش دارد.
و اما مهمترین کاربرد ضریب تغییرات برای ما، کاربرد آن برای اقتصاددانها، مدیران مالی و سرمایهگذاران در حوزههای مرتبط با سنجش ریسک و ریوارد و پراکندگی آنها است.
در امور مالی، ضریب تغییرات به سرمایهگذاران اجازه میدهد تا مقدار ریسک و نوسان آن را در مقایسه با بازده مورد انتظارشان (r) تعیین کنند.
فرمول محاسبه ضریب تغییرات
همانطور که پیشتر بیان کردیم، ضریب تغییرات نشاندهندهی انحراف معیار از میانگین است. بنابراین فرمول آن به این صورت است:
و نحوه محاسبه میانگین:
(البته ما قصد نداریم اینجا آمار درس بدهیم، ولی برای کامل بودن مطلب و آشنایی ابتدایی با ادبیات موضوع، باید لااقل سطوح ابتدایی تعریفها را ذکر کنیم)
اکنون با یک مثال، نحوه محاسبه ضریب تغییرات در یک مجموعه داده را مرور میکنیم:
سن دانشجویان یک کلاس، به صورت زیر است:
20، 25، 32، 18، 22
ضریب تغییرات آن را محاسبه میکنیم:
مقایسه ضریب تغییرات و انحراف معیار
انحراف معیار ابزاری آماری است که پراکندگی یک مجموعه داده را نسبت به میانگین آن مجموعه اندازه میگیرد. بنابراین به جای مقایسهی دادهها باهم، میزان پراکندگی مقادیر آن جامعه آماری را محاسبه میکند.
اما وقتی بخواهیم چند مجموعه داده را باهم مقایسه کنیم، ضریب تغییرات کارایی بیشتری دارد. CV نسبت انحراف معیار به میانگین است و چون مستقل از واحدی است که اندازهگیری در آن انجام شده، میتوان از آن برای مقایسه چند مجموعه داده، که ممکن است بعضاً جنس واحدهای آنان بسیار متفاوت باشد، استفاده کرد.
به طور خلاصه، انحراف معیار میزان پراکندگی موجود حول میانگین یک مجموعه را اندازهگیری میکند، در حالی که ضریب تغییرات نسبت انحراف معیار به میانگین را اندازهگیری میکند.
بنابراین کاربرد اصلی انحراف معیار برای محاسبات صرفاً درون یک مجموعه است (یا چند مجموعه ولی با جنس کاملاً یکسان). اما کاربرد اصلی ضریب تغییرات در مقایسهی میان گروههای متفاوت باهم است.
به عنوان مثال میخواهیم میزان پراکندگی سن (برحسب سال) و قد (برحسب سانتی متر) یک کلاس 100 نفره را باهم مقایسه کنیم. میانگین قدی این گروه برابر با 170 سانتی متر و دارای انحراف معیار 17 سانتی متر است. همچنین میانگین سنی افراد این کلاس 20 سال، با انحراف معیاری 2 ساله است.
بنابراین ضریب تغییرات سن و قد افراد این کلاس برابر است. به این معنی که میزان پراکندگی سن افراد کلاس حول میانگین که 20 باشد، برابر با میزان پراکندگی قد افراد این کلاس حول میانگین 170 سانتی متری آنها است.
کاربرد ضریب تغییرات در بازارهای مالی
یکی از مهمترین و کاربردیترین شاخصهای آماری برای محاسبهی ریسک یک دارایی، انحراف معیار است. همانطور که پیشتر هم گفتیم، انحراف معیار به بررسی میزان پراکندگی حول میانگین میپردازد. در فرایند محاسبه ریسک، انحراف معیار مقادیر مختلف بازده یک دارایی را حول بازده مورد انتظار سرمایهگذار، اندازهگیری مینماید.
منظور از بازده مورد انتظار، میزان بازدهای است که یک دارایی به احتمال زیاد کسب خواهد کرد. این بازده به این طریق به دست میآید:
در این حالت انحراف معیار به صورت زیر درمیآید:
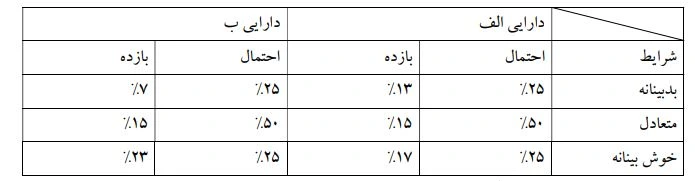
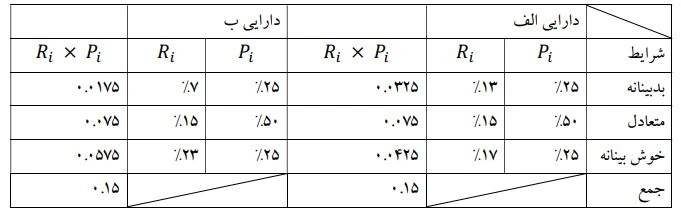
به عنوان مثال برای 2 دارایی الف و ب، حالات و احتمالات زیر وجود دارد:
مطلوب است محاسبه ریسک هر دارایی.
ابتدا بازده مورد انتظار R را محاسبه میکنیم:
احتمال وقوع همان Pi است. بازده هر حالت هم Ri است. بنابراین:
بنابراین بازده مورد انتظار هردو دارایی 15% است.
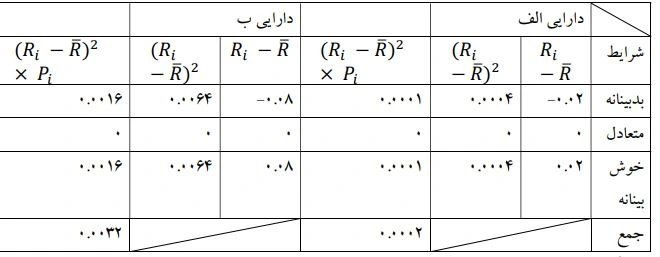
در ادامه انحراف معیار را طبق فرمول محاسبه میکنیم:
با جایگذاری در فرمول، انحراف معیار دارایی الف و ب به دست میآید:
بالاتر بودن انحراف معیار دارایی ب، به معنی بالاتر بودن ریسک دارایی ب نسبت به دارایی الف است:
زیرا هرچه انحراف معیار بالاتر باشد، به معنی پراکندگیهای بیشتر در حول میانگین است. پس در دارایی ب، پراکندگی و اختلاف حول بازده مورد انتظار، بیشتر از پراکندگی بازده دارایی الف است. پس دارایی ب ریسک بیشتری را به سرمایهگذار تحمیل میکند.
ضریب تغییرات و ریسک به سود
در امور مالی، ضریب تغییرات در انتخاب میان گزینههای سرمایهگذاری مهم است. فرمول ضریب تغییرات در امور مالی، نشاندهندهی نسبت معروف “ریسک به سود ” یا همان “ریسک به ریوارد” است.
در این صورت ضریب تغییرات، نوسان ریسک یک سرمایهگذاری را در برابر پاداش آن سرمایهگذاری نشان میدهد.
در مثال قبلی:
بنابراین میزان ریسک به ریوارد دارایی ب بیشتر از دارایی الف است. معنی این عبارت این است که اگر دارایی ب را بخریم، برای به دست آوردن یک مقدار سود معین، باید میزان ریسک بسیار بیشتری را متحمل شویم، نسبت به حالتی که اگر دارایی الف را میخریدیم.
کاربرد ضریب تغییرات در انتخاب گزینه سرمایهگذاری
همواره برای سرمایهگذاری گزینههای مختلفی در دسترس هستند، بازار سهام، ملک، طلا، رمزارزها و … . اما انتخاب یک یا چند گزینه از میان اینها، نیازمند دقت در مفهوم ریسک به ریوارد است.
به صورت خلاصه، ریسک به ریوارد به شما یا سبدگردانتان میگوید که حاضر هستید چه میزان ریسک را برای به دست آوردن سود تحمل کنید. معمولاً سبدگردانها برای تعیین این مقدار، از سرمایهگذاران سؤالاتی میکنند یا چالشهایی را پیش روی شخص میگذارند، تا توسط پاسخهای سرمایهگذار، بتوانند میزان ریسکپذیری او در مقابل سود مطلوب او را به دست بیاورند.
از یک مقداری به بعد، هرچه میزان ریسک به ریوارد بالاتر باشد، سرمایهگذاری توجیه اقتصادی و منطقی خود را از دست میدهد. که این موضوع به ریسکپذیری یا ریسکگریزی سرمایهگذار نیز بستگی دارد.
به طور مثال میخواهیم با توجه به دیتاهای (فرضی) تاریخی بازارهای ایران، گزینهی سرمایه گذاری انتخاب کنیم:
بر فرض شاخص بورس ایران در 20 سال گذشته، حدوداً سالی 55% بازدهی داده باشد و انحراف استاندارد آن 18% بوده باشد. از طرف دیگر خرید و نگهداری سکهی طلا در این 20 سال، حدوداً سالی 50% بازدهی داشته باشد، با انحراف معیاری معادل 20%. گزینهی دیگر خرید ملک باشد که بازدهی سالانه 60% داشته با انحراف معیار 32%.
ضریب تغییرات شاخص بورس، کمتر از ضریب تغییرات دیگر بازارها بوده است. بنابراین سرمایهگذاری در میانگینِ بورس ایران، نسبت ریسک به ریوارد کمتری در قیاس با بازارهای دیگر داشته، در نتیجه گزینهی مناسبتری برای سرمایهگذاری بوده است.
محاسبه ضریب تغییرات در اکسل
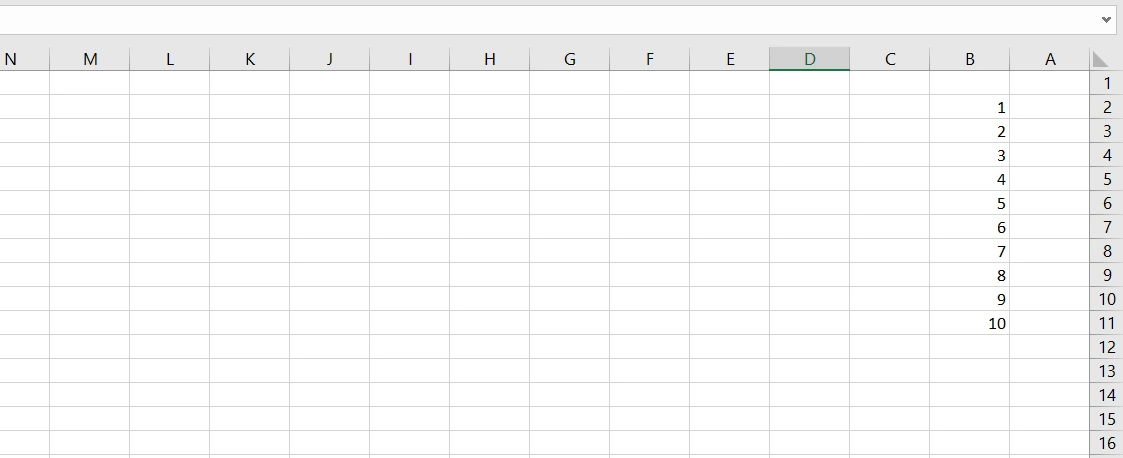
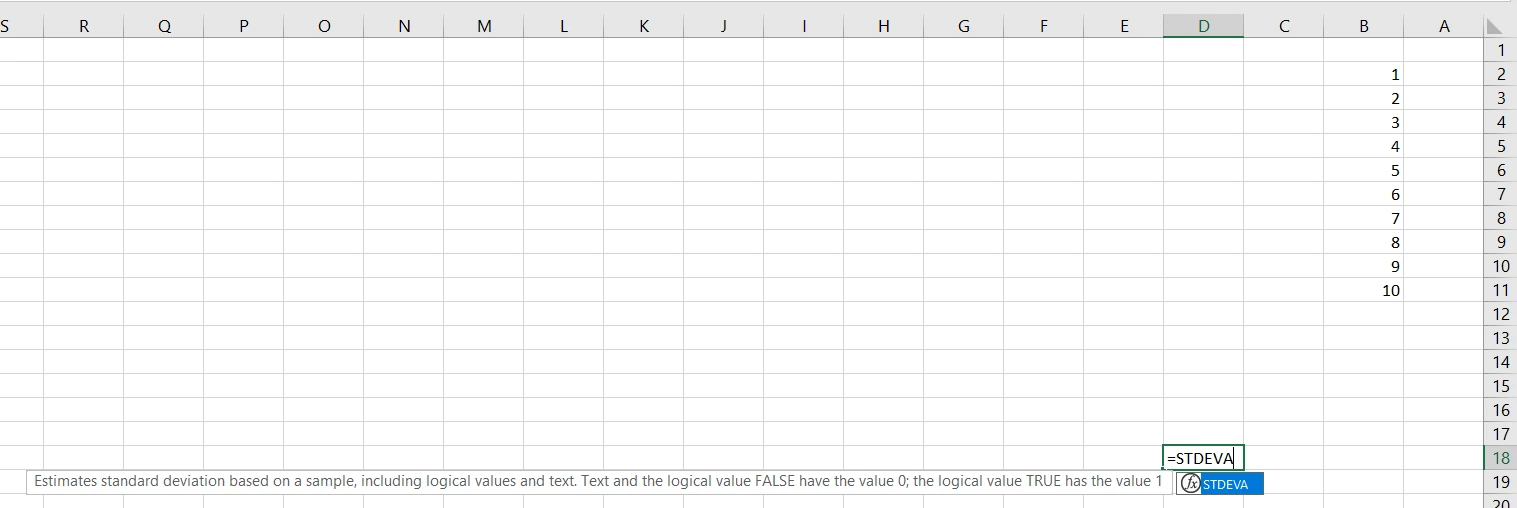
برای محاسبه کردن ضریب تغییرات در اکسل، ابتدا لازم است دادههای جامعه آماری مد نظرمان را در یک ستون اکسل ثبت کنیم. من در این ستون اعداد 1 تا 10 را به ترتیب وارد کردم. یعنی فرض میکنم جامعه آماری من اعداد 1 تا 10 است.
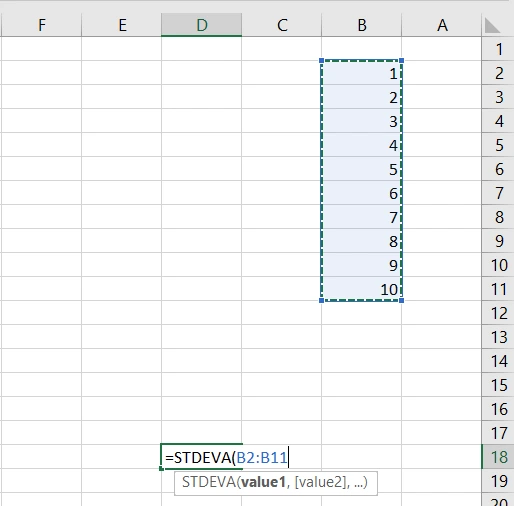
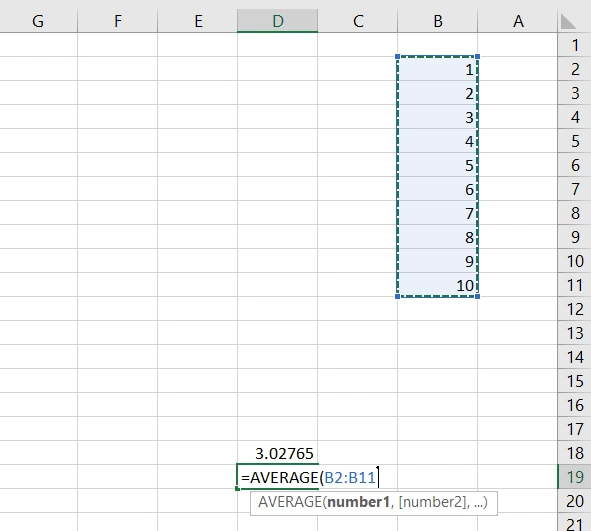
در اکسل دستور STDEVA برای محاسبه کردن انحراف معیار در یک جامعه آماری است. پس این دستور را در یک سلول وارد میکنم. همزمان با وارد کردن این دستور، مثل اکثر دستورهای دیگر اکسلی، از ما میخواهد دادهها را مشخص کنیم:
بنابراین ستون دادهها (در این مثال اعداد 1 تا 10) را به صورت کامل انتخاب و به اکسل معرفی میکنم:
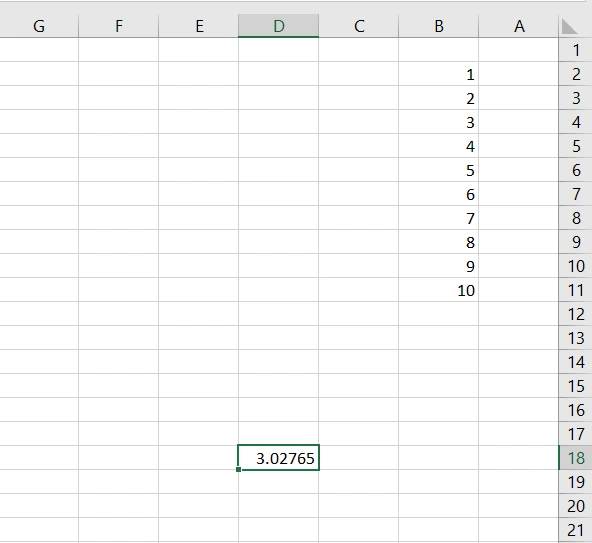
سپس برای تأیید و اجرای دستور، اینتر را میزنیم و اکسل نتیجه را به ما نشان میدهد:
بنابراین انحراف معیار جامعه آماری 1 تا 10، برابر با 3.027 شده است.
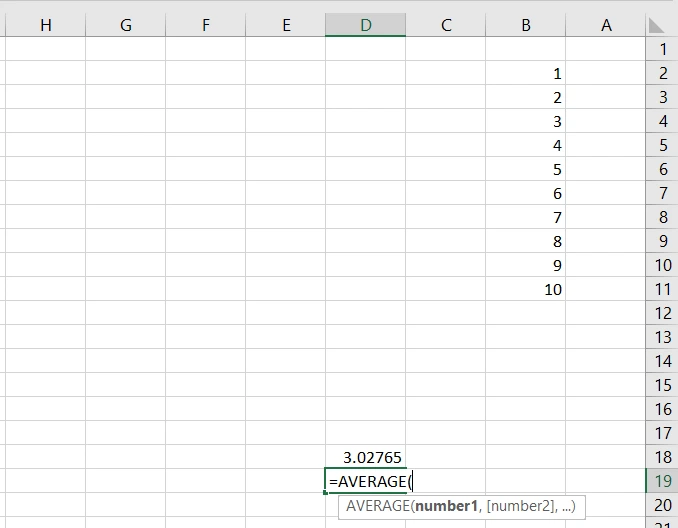
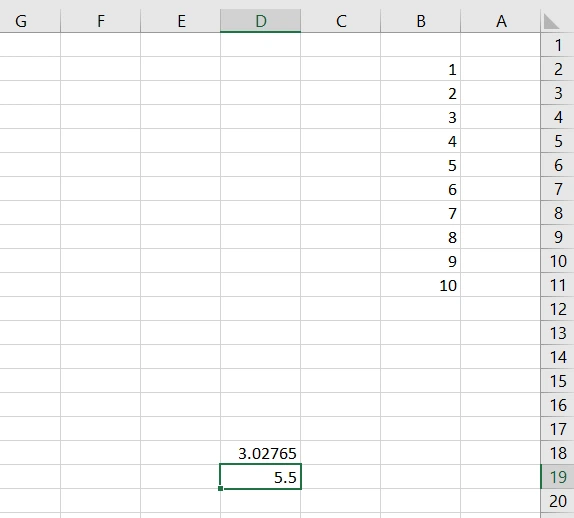
اکنون نوبت محاسبه کردن میانگین است. برای محاسبه میانگین در اکسل، باید دستور AVERAGE را بنویسیم:
سپس جامعه آماری 1 تا 10 را انتخاب میکنیم:
اینتر را زده و دادهها را تأیید میکنیم و اکسل نتیجه محاسبه میانگین را به ما نشان میدهد:
بنابراین میانگین دادههای ما برابر با 5.5 است.
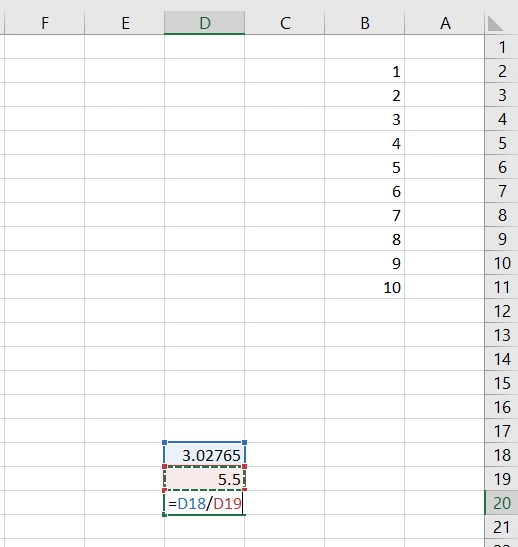
در آخرین گام فقط لازم است سلول انحراف معیار را بر سلول میانگین تقسیم کنیم:
همانطور که در تصویر بالا نشان داده شده، ما سلول D20 را برای اینکار انتخاب کرده و در آن سلول، دستور تقسیم انحراف معیار (D18) بر میانگین (D19) را تایپ کردیم.
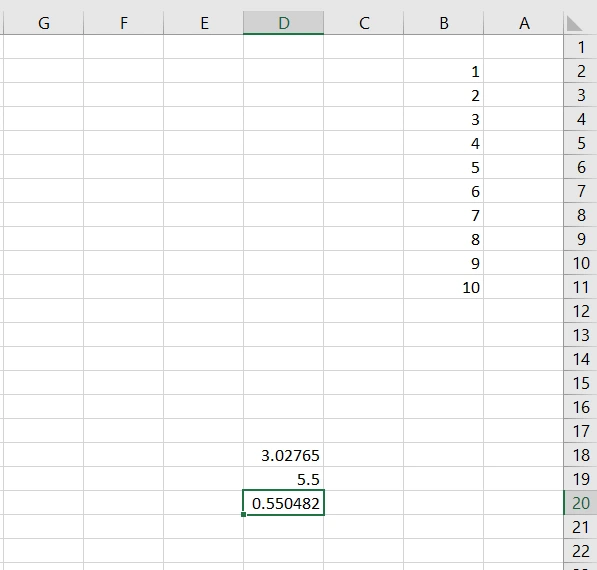
نتیجهی این عبارت، برابر با ضریب تغییرات دادههای ما است:
پس ضریب تغییرات جامعه آماری با این روش به دست میآید، که در این مثال برابر با 0.55 است.
در صورتی هم که بخواهیم میان چندین گزینه سرمایهگذاری به کمک اکسل، بهترین آن را انتخاب کنیم، کافی است به جای دادهها از ریسک و ریوارد در اکسل استفاده کنیم.
سخن آخر
ضریب تغییرات یک روش ساده برای مقایسه میزان پراکندگی یک سری داده در برابر سری دیگر است. تقریباً میتوان آن را به راحتی محاسبه کرده و برای هر موضوعی اعمال کرد، از جمله فرآیند انتخاب سرمایهگذاری مناسب.
به طور کلی امروزه و در دنیای سرمایهگذاری مدرن، نمیتوان خیلی غیرعلمی کار کرد و خیلی هم دوام آورد. بنابراین بهتر است تا بازار ما را با زیانهای وحشتناک تنبیه نکرده و مجبور به آموختنمان نکرده است، خودمان دست به کار شده و بیاموزیم!
منابع:کورپوریت فایننس